Choosing batteries for an electronic box
The choice of batteries for an electronic box is important, and many myths prevail on the topic, such as including the resistance of the atomizer. You will find the right formula below.
In simple terms
To give you an explanation, this article will have to get a little technical, or at least use some physics formulas. If you don’t want to get bogged down in details, but simply want to know how to choose your batteries, below is a table indicating the current (in amperes) drawn from each of the batteries in your box based on your vaping power. This is the main parameter to help you choose your batteries.
The four tables: “1 battery”, “2 batteries” etc. indicate how many batteries are in your box. Select the relevant table for your needs.
Each contains two rows. In the “Watts” row, you will find the max power of your box, or preferably your max vaping power, within a margin: if you never vape above 45 W, go for 50.
Just below that in the “Amp/battery” row, you will find the max current in Amperes drawn from each of your batteries (or battery if there is only one).
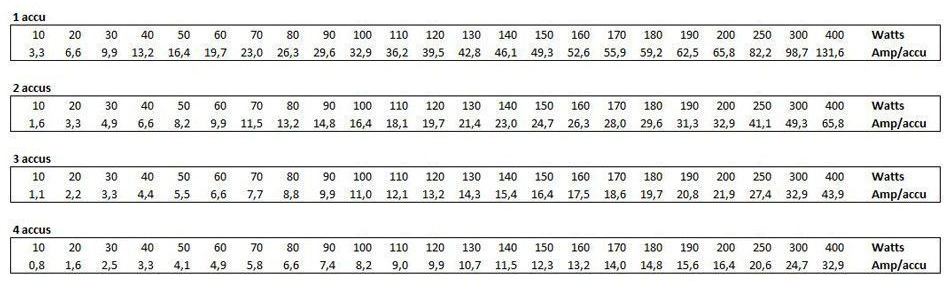
For example, for an 80 W double-battery box (and therefore the “2 batteries” table), you will draw a maximum of 13.2 amperes from each of the batteries. You then simply need to go to the “Recommended batteries” section at the end of this article to make your choice based on what you now know to be the amperage requirement for your batteries.
And yes, this calculation does not include the set-up resistance, which is of no impact with an electronic box; the same can be said for the serial or parallel configuration of the batteries. If you want to understand why, we are now going to get your brain cells working.
Ohm’s Law with mechs
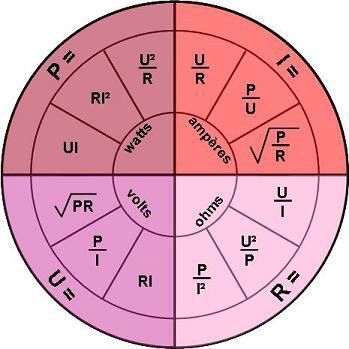
Many errors stem from applying the specific rules of mech mods to electronic mods. In both cases, Ohm’s Law applies, but in a different way, which changes the results considerably.
In a mech mod, the battery is in direct contact with the resistance coil. Ohm’s Law can be applied using the formula I=U/R, i.e. the current (in amperes) is equal to the voltage (in volts) over the resistance (in ohms).
The lower the resistance of the set-up, the more power (more watts) it will receive, and the greater the current demand (in amperes) from the battery. The more the battery is depleted, the lower the output in current and power.
In the case of mech boxes with multiple batteries, the distinction between serial and parallel set-ups is also critical. In one case, the current drawn from each battery will be split, and the max discharge currents (MDC) may be added. In the other, the voltages are added without adding the MDC values. All users of mech mods know (or should know) this.
In sum, the battery configuration (serial or parallel) and the resistance of the set-up (therefore Ohm’s Law) are key factors to be taken into account with mech mods. And you will have learned nothing new if you use a mech and you don’t want to end up on the news with a hole in your hand; claiming otherwise would be simply dangerous.
You will often encounter this conventional reasoning and these calculations being applied to electronic boxes. Unfortunately, this approach doesn’t work, and that’s precisely the point.
Ohm’s Law with electronic boxes
Here’s a trick question: what is the resistance applied to the battery terminals in an electronic mod? Not that of the set-up, but that of the chipset, the electronic circuit of the box, that you have no way of knowing! So how can you apply Ohm’s Law in the same way as with a mech mod if you don’t know the resistance at the battery terminals?
It’s simple. The resistance of your set-up doesn’t matter: the batteries are in contact with the chipset. That makes all the difference. And for batteries, the difference is huge.

Ohm’s Law obviously still applies, but this time in the format I=P/U, i.e. the current is equal to the power divided by the voltage. It makes sense: the issue of resistance doesn’t come up, and it is not known in any case (once again at the battery terminals, so that of the chipset).
However, power comes into play, which is a good thing, as that’s what is set on an electronic box.
The battery voltage is also a factor, and we will see how.
As we are talking about power, the serial or parallel configuration of the batteries is completely irrelevant. An output of 60 W would represent 30 W per battery if you have two, 20 W per battery if you have three, and 15 W per battery if you have four, regardless of how they are set up. The power is split equally between the batteries; it doesn’t matter how they are configured.
To determine the current required in an electronic box, the calculation is therefore I=P/U, which is adapted to obtain the current required from each battery:
Current per battery = (power set in watts on the box / number of batteries) / battery voltage.

In short, it all depends on the power set on your box, the number of batteries and the current voltage of each battery. And, we would like to stress once again, absolutely not on the resistance of your set-up, or the battery configuration. The latter obviously changes the voltage applied to the chipset, and manages that sent to the set-up differently depending on whether the input is 8.4 or 4.2 V, but it only concerns the internal operation of the chipset, which is of no interest in this case.
Therefore, if you have a double-battery box, the batteries are charged (4.2 v) and you set your box to 60 W, you will draw (60/2)/4.2= 7.14 A from each of the batteries, whether the configuration is serial or parallel.
With the same setting but with discharged batteries, let’s say at 3.5 V, this value will be (60/2)/3.5 = 8.57 A per battery. The process is the reverse of that of a mech mod, the chipset draws more from the batteries when their charge is lower. That makes sense as you need to output the same power with less input voltage as when the battery is fully charged.

It is also worth noting that for mods indicating an amperage, the value given is that of the set-up, not that on the batteries. You will also note that it corresponds to the conventional version of Ohm’s Law, that of mech mods. If you calculate the amperage with the claimed resistance and voltage, you will get the same value as that on the screen. It is completely irrelevant in our case, and you won’t need to use it to choose your batteries.
For example, a double-battery box, with the batteries charged at 4.2 V, a 0.5 Ω set-up and power of 60 W. The chipset will output 5.48 V and 10.95 A to the resistance coil, with these values being displayed. On the other hand, it will draw 7.51 A from each battery, the value which is of interest in this case, and which is not on the screen.
To be more precise, the formula should also account for the efficiency of the chipset, i.e. account for the loss generated by the chipset itself. Chipsets are frequently assumed to have a 95% efficiency, so 5% is lost. This is a somewhat optimistic value, in fact, it is more likely to be around 85 or 90%, but we are going to start from there.
You therefore need to divide the previous result by 95%, so the complete formula is now
Current per battery = (power set in watts on the box / number of batteries) / battery voltage) / 0.95
On a calculator, enter in the following order:
Max power / number of batteries / min voltage / 0.95 =
How to choose your batteries for an electronic box
So, how do you choose your batteries for an electronic box? It all depends on the number of batteries in your box and your vaping power. Take the max power that you will be using, or the max power of the box if you intend to use that.
The max current requested from each of your batteries is calculated as follows:
Max current per battery = ((max power on box / number of batteries in box) / Min battery voltage) / 0.95

The min battery voltage is the box cutoff voltage. When the batteries drop to the min voltage, the box will display something like “low batteries” and switch off. This value is quite easy to find: measure the battery voltage when the box tells you to charge the batteries. If you are unable to measure it, take 3.2 V, you shouldn’t be too far off the mark.
Some boxes measure the charge voltage and switch off when it drops to 2.8 V. If you want to have some leeway, use this value in your calculations.
Based on this calculation, for a 75 W single-battery box, the requirement from the battery is ((75/1)/3.2)/0.95=24.67 amperes when it reaches 3.2 V. This is the maximum value for most 25R style batteries, which explains why most single-battery boxes do not go over 75 W (at least not for very long), and recommend 25 A batteries.
This value can be found with the rated (average) battery voltage which is 3.6 V, giving 72 W at 20 A, the limit of most direct current batteries. The limit of 75 W per battery is obviously the ideal limit that boxes can draw from batteries.

This also explains why many double-battery boxes initially stopped at 150 W, which was the sensible limit. For marketing purposes, manufacturers have pushed back the limit to 200 W, representing ((200/2)/3.2)/0.95=32.89 A per battery when they reach 3.2 V. That’s a bit much.
This is explained by the fact that the box will not deliver 200 W with low batteries, and that on account of the voltage sag (the difference between the no-load voltage and the on-load voltage of a battery), you will get a longer battery life at 200 W using a 1500 mAh/30 A battery than with a 3000 mAh/20 A.
Yes, but in that case, why can 200 W boxes only output at low resistances, if the set-up resistance is not a factor? That’s a good question, even if I do say so myself. The set-up resistance is a factor in the chipset, which is required to output the 200 W mentioned above. A sufficient output voltage is needed, and the higher the set-up resistance, the higher this voltage needs to be. The conventional version of Ohm’s Law returns, since we are talking about the resistance and the chipset. To get 200 W with a 0.4 Ω set-up, the box needs to deliver 9 V, very few boxes can manage more. This value is the max voltage limit of the chipset, not the battery.
Yes (of course!), but some boxes will not be able deliver 200 W if the resistance is too low either! Good point, but we are talking about the chipset output amperage limit. At 200 W, with a resistance of 0.1 ohm, the chipset is supposed to deliver 45 A, which is huge. And 63 A with a resistance of 0.05 ohm once again at 200 W. The chipset limit is again a factor, this time for the output amperage.
However, if you vape at not more than 40 W and you have chosen a double-battery box for battery life reasons, you can go one step better and choose batteries with a higher capacity (mAh), the fact that their max “amperage” is lower won’t be a problem: for 40 W with a double-battery box, you will never request more than 7.5 A from each battery, if at all if the box drops them to 2.8 V! You can use a 3300 mAh/10 A battery without any problems, and get more battery life than with a conventional 2500 mAh/20 A.

It is also worth noting that the set-up resistance is not a factor in the calculation. That implies that it has no influence on the battery life of the box! If you are unsure: the capacity (hence battery life) of a battery is measured in milliamperes per hour: the battery can deliver this number of milliamperes for one hour. The amperes drawn from the battery are not dependent on the set-up resistance. Hence, neither is the battery life: it depends on the amperage drawn from the battery, which in itself is not dependent on the set-up resistance.
Therefore, you will get exactly the same battery life, at equal power, when vaping with a 1 Ω set-up or with a 0.2 Ω set-up. So there is no need to have set-ups with a higher resistance to get more battery life, this s pointless with electronic boxes. The same applies for both the power mode and the temperature control.
You now know how to calculate the acceptable “amperage” so that your batteries run properly in your electronic box, based on your use. This is important: boxes detect a battery overload indirectly. However, on one hand, your vaping experience will not be pleasant if your box keeps switching off, and, on the other, if this protection doesn’t work, your batteries may degas or, even worse, explode, even though the risk is tiny.
To find out more…
Batteries are a huge topic; we have written a series of articles examining the question.
- As straightforward as it might be, battery charging requires some pointers and was well worth devoting an article to help you do so safely and effectively.
- Buying the right battery is good, but keeping it longer is even better! For this reason, we have compiled a comprehensive tutorial on extending the service life of your batteries.
- However, a drop in battery performances, a battery impact or breach of the protective sleeve is bound to happen eventually. It is important to know when to replace a battery and how to dispose of it.
- For those who want to find out more, our article on key battery characteristics explains everything you need to know about the battery capacity and maximum discharge current, and how they are determined.
- And if you want to understand how to optimise your battery choice and use, our article on battery specifications goes into more detail on the concepts of internal resistance, voltage sag, rated voltage, and provides details on the different chemistries.
- On another note, an article on e-cigarette battery explosions. As the media feast on these stories, despite them being extremely rare, we thought it was important to review this explosive topic to understand it, and above all prevent it from happening to you.
Don’t forget!
- Never use a battery beyond its specifications, both for battery life and your safety.
- Always carry batteries in suitable protection; most of the rare accidents that occur are linked with transporting unprotected batteries.
- Only use batteries that are in perfect condition, free from scratches or impacts.
- Never throw a battery away, place it in a specific recycling container.